결정이론
새로운 값 x가 주어졌을 때 확률모델 $p(x,t)$ - (input x, 목표값 t)에 기반해 최적의 결정(예를 들어 분류) 을 내리는 방법론
추론 단계: 결합확률분포를 구하는 것이고
결정 단계: 확률이 주어졌을 때 어떻게 최적의 결정을 내릴 지
->
우도와 사전확률을 최대화 시키는 것이 이 확률을 높이는 데에 도움이 될 것
->
직관적으로, 조건부확률을 최대화시키는 k를 찾는 것이 가장 좋은 결정
->
최적의 결정 영역을 찾는 것이 목표
예: x-ray 이미지를 보고 암 판별하기
-> 직관적으로 볼 때 $p(C_k|x)$ 를 최대화 시키는 $k$를 구하는 것이 좋은 결정
암진단 예시에 대한 보다 상세한 설명: 베이즈 정리- 예제 1, 2 참고
https://angeloyeo.github.io/2020/01/09/Bayes_rule.html
이진 분류 예시
결정영역 $Ri = \{x : pred(x) = Ci\}$ (클래스 i에 속하는 모든 x의 집합)
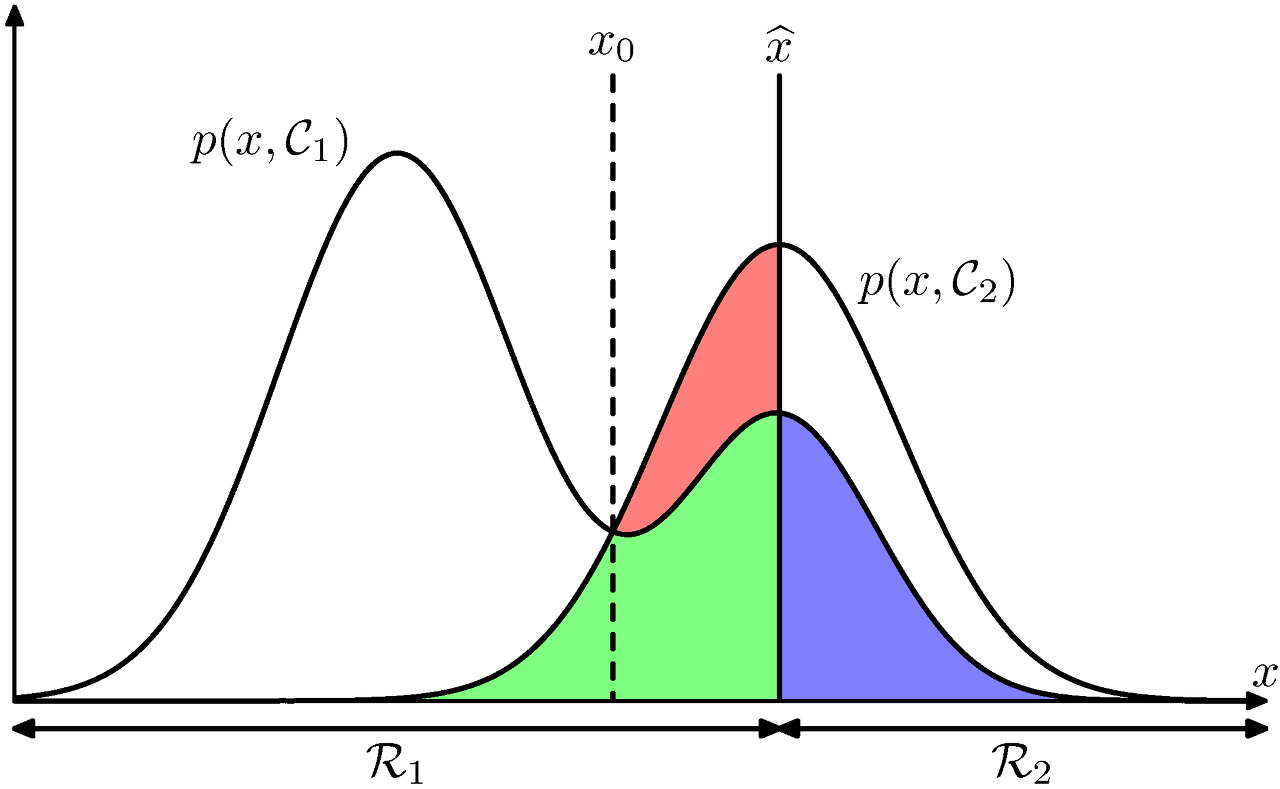
위와 같은 결합확률분포 그림에서, 분류의 기준을 $\hat{x}$이라고 했을 때
분류오류의 확률
1. 영역 $R1$에 속하는 $x$를 클래스 $C2$로 분류했을 때(빨간 + 녹색)
2. 영역 $R2$의 $x$를 클래스 $C1$로 분류(보라)했을 때
$p(mistake)=p(x\in R_1, C_2) + p(x\in R_2, C_1)=\int_{R_1}p({\bf x}, C_2)d{\bf x} + \int_{R_2}p({\bf x}, C_1)d{\bf x} \qquad$
->
분류기준을 $\hat{x}$에서 $x0$로 옮긴다면 빨간색 영역이 제거되면서 오류를 최소화 (에러는 여전히 남아있지만 최대한 줄인 곳)
각각의 x에 대해 $C1$의 확률과 $C2$의 확률을 비교해보고, $p(x, C1)$ > $p(x, C2)$인 경우 $R1$에 할당을 하면 됩니다.
$p(C1|x)$ > $p(C2|x)$ 인 경우 분류오류의 확률을 최소화 시킬수 있음
Multiclass 경우
오류를 생각하는 것보다 얼마나 정확한가를 생각하는게 더 편할 수 있음
결정영역 $Ri$와 클래스 $Ci$가 일치하는 확률을 모두 더해 얼마나 정확한지에 대한 확률을 구할 수 있다. 그리고 $x$가 주어졌을 때 조건부확률 $p(Ck|x)$가 최대가 되는 영역 $Rk$에 클래스를 분류하면 정확도가 가장 높다고 볼 수 있다.
K개의 클래스가 있을 경우, 각각의 결정영역 $Ri$마다 결정영역과 실제 클래스 $Ci$가 일치하는 확률을 모두 더해 얼마나 정확한지에 대한 확률을 구할 수 있다.
어떻게 하면 최적의 결정을 내릴 수 있을까?
-> $x$가 주어졌을 때 조건부확률 $p(Ck|x)$가 최대가 되는 영역 $Rk$에 클래스를 분류하면 정확도가 가장 높다.
$p(correct)=\sum_{k=1}^{K}p(x \in R_k, C_k) = \sum_{k=1}^{K}\int_{R_k}p(x, C_K) d{\bf x} \qquad$
$pred(x)$ = $argmax_k{p}$$(Ck|x)$
결정이론의 목표 (분류의 경우)
결합확률분포 $p(x,C_k)$ 최적의 결정영역들을 찾는 것
$\hat{C}$$(x)$ 를 $x$가 주어졌을 때 1부터 $K$까지의 예측값중 하나를 돌려주는 함수라고 할 때, 최적의 함수 $\hat{C}$$(x)$를 찾는 것
$x$가 $Rj$ 에 속하면 $\hat{C}$$(x)$ 의 값이 $j$인 경우 결합확률분포 $p(x,C_k)$ 가 주어졌을 때 최적의 함수 $\hat{C}$$(x)$ 찾기
--> 그렇다면 어떤 기준으로 최적의 함수를 찾을 것인가?
기대손실 최소화(Minimizing the Expected Loss)
- 모든 결정이 동일한 리스크를 갖는 것이 아니다. ex> 암이 아닌데 암으로 진단 or 암인데 암이 아닌 것으로 진단 -> 후자가 훨씬 큰 리스크 / 코스트
- 리스크의 정도를 정형화 시켜 표현하기 위해 손실행렬(loss matrix)를 가정
- $L_k{_j}$(손실행렬) : $C_k$에 속하는 $x$ 를 $C_j$로 분류할 때 발생하는 손실 또는 비용.
- 다음과 같은 기대손실을 최소화하는 것을 목표로한다.
$\mathbb{E}$$[L]$ $= \sum_{k}\sum_{j}\int_{R_j}L_{kj}p({\bf x}, C_k)\;d{\bf x} \qquad$
모든 가능한 결정에 대해 그 손실값을 결합확률에 곱한 값을 적분한 값
$\hat{C}$$(x)$ = $argmin_j$$\sum_{k=1}^{K} L_{kj}p$$(C_k|x)$
만약에 손실행렬이 0 - 1 loss인 경우 (주대각선 원소들은 0, 나머지는 1)
$\hat{C}$$(x)$ = $argmin_j$$1-p(C_j|x)$
= $argmax_j$$p(C_j|x)$
예제 : 의료진단
암인데 암이 아닌 것으로 진단했을 때의 오진단의 리스크가 크기 때문에, 조금 더 안전한 진단을 하기 위해서는 손실행렬을 모델안에 포함시켜서 계산해야
$C_k \in \{1,2\}$ ${\Leftrightarrow}$ $\{sick, healthy\}$
$L = $ $\begin{bmatrix} 0&100 \\1 &0 \end{bmatrix}$
$\mathbb{E}$$[L]$ $=\int_{R_2}L_{1,2}p({\bf x}, C_1)\;d{\bf x} \qquad$ + $\int_{R_1}L_{2,1}p({\bf x}, C_2)\;d{\bf x} \qquad$
$=\int_{R_2}100\times$$p({\bf x}, C_1)\;d{\bf x} \qquad$ + $\int_{R_1}p({\bf x}, C_2)\;d{\bf x} \qquad$
$j = 1$ 일때
$\sum_{k=1}^{K} L_{k,1}p$$(C_k|x)$ = $L_{11}p( C_1|k)$ + $L_{21}p( C_2|k)$
= $p( C_2|k)$
$j = 2$ 일때
$\sum_{k=1}^{K} L_{k,2}p$$(C_k|x)$ = $L_{12}p( C_1|k)$ + $L_{22}p( C_2|k)$
= 100$p( C_1|k)$
--> 둘을 비교해서 $p( C_2|k)$ > 100$p( C_1|k)$
결정이론 (회귀문제의 경우)
목표값 $t \in R$ (분류 문제와는 다르게 $t$는 실수
손실함수 $L(t, y(x))$ =$ \{ y(x) - t\}^2$
$F[y] = $ $E[L] = $ $\int{_R} \int{_x} $ $\{y(x) -t\}^2$$p({\bf x}, t)d{\bf x}dt$
$=\int_{x}(\int_{R}\{y({\bf x})-t\}^2p({\bf x}, t)dt)dx$
$=\int_{x}(\int_{R}\{y({\bf x})-t\}^2p(t|{\bf x})dt)p(x)dx$

${\bf x}$를 위한 최적의 예측값은 $y(\bf x)$ = $\mathbb{E}_t[t|x]$ 임을 보일 것이다.
즉, 조건부 x에 대한 t값의 평균 -> 회귀의 결과와 동일
Euler - Lagrange Equation
Euler -Lagrange Equation을 통해 손실함수의 기댓값을
최소 로 하는 y(x)를 구할수 있다.
참고 : 오일러-라그랑주 방정식
오일러-라그랑주 방정식 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 오일러-라그랑주 방정식(Euler-Lagrange方程式, Euler–Lagrange equation)은 어떤 함수와 그 도함수에 의존하는 범함수의 극대화 및 정류화 문제를 다루는 미분 방정식이
ko.wikipedia.org
차원 오일러-라그랑주 방정식 유도는 수학에서 고전으로 꼽힌다. 이 증명의 근거는 변분법의 기본정리이다.
함수 $ y$ 가, 경계값 조건 y(a) = c, y(b) = d를 만족하고, 다음과 같이 주어지는 범함수 $F[y]$ 를 최대 또는 최소로 만든다고 하자.
${F[y]=\int _{a}^{b}G(x,y(x),y'(x))\,dx.\,\!}$
여기서 $G$가 연속적인 편미분값을 가진다고 가정한다. (가정을 더 약하게 잡을 수도 있으나, 그러면 증명이 더 복잡해진다.)
만일 $y$가 상대 범함수를 최대, 최소로 한다고 하면 $y$에 매우 작은 변화를 가했을 때,$F[y]$ 의 값이 늘거나($y$ 가 $F[y]$ 를 최소화할때) $F[y]$ 의 값이 줄 수 있다.($y$가 $F[y]$를 최대화할때)
좀 더 정리하기 위해, 두 번째 항에 부분적분을 한다. 그러면 다음과 같은 식을 얻는다.
${\frac {\partial F}{\partial y(x)}}$ = ${\frac {\partial G}{\partial y}}-{\frac {d}{dx}}{\frac {\partial G}{\partial y'}}$
For regression,
$F[y] = $ $E[L] = $ $\int{_R} \int{_x} $ $\{y(x) -t\}^2$$p({\bf x}, t)d{\bf x}dt$
$=\int(\int\{y({\bf x})-t\}^2p({\bf x}, t)dt)dx$
$=\int(\int\{y({\bf x})-t\}^2p(t|{\bf x})dt)p(x)dx$
결정문제를 위한 몇가지 방법들
분류문제의 경우
확률모델에 의존하는 경우는 생성모델, 식별모델을 사용할 수 있음.
- 생성모델: 각 클래스 Ck에 대해 분포 p(x|Ck)와 사전확률 p(Ck)를 구한다음 베이즈 정리를 사용해서 사후확률 p(Ck|x)를 구함
- 식별모델: 모든 분포를 다 계산하지 않고, 오직 사후확률 p(Ck|x)를 구합니다.
생성모델을 하는 경우 많은 확률들을 구해놓으면 유연하게 대처할 수 있음
확률이 달라질 경우 이전에 구했던 파라미터들을 재생시켜서 더 쉽게 다시 구할 수 있음.
확률모델에 의존하지 않고, 판별함수에 의존하는 경우는 입력 x를 클래스로 할당하는 판별함수를 찾는 것
회귀문제의 경우
결합분포 p(x,t)를 구하는 추론 문제를 먼저 푼 다음 조건부확률분포를 구함
그 후 주변화(marginalize)를 통해서 Et[t|x]를 구함
'Machine Learning' 카테고리의 다른 글
| [AI class w7d4] Linear Model for Classification 선형분류 TIL (0) | 2021.06.14 |
|---|---|
| [AI class w7d3] Linear Model for Regression 선형회귀 TIL (0) | 2021.06.09 |
| [AI class w6d5] Week6 과제 ML Basics 실습 (0) | 2021.06.07 |
| [AI class w6d3] E2E - linear regression ML 처음부터 끝까지 (0) | 2021.06.03 |
| 머신러닝 AI 이론, 수학 공부에 큰 도움이 된 블로그 모음 (0) | 2021.06.01 |